Im Jahr 2017 wurde auf dem Preprint Server arXiv eine Arbeit mit dem Titel «On a Formal Model of Safe and Scalable Self-driving Cars» von Shalev-Schwartz, Shammah und Shashua publiziert. In diesem Artikel wird ein deterministisches Sicherheitsmodell namens RSS für selbstfahrende Autos präsentiert, welches zu garantieren behauptet, dass es keine Unfälle mehr gibt, wenn alle Verkehrsteilnehmer die durch RSS definierten Regeln respektieren. Das Ziel des Projektes bestand darin, die physikalischen und mathematischen Behauptungen im Artikel zu validieren resp. Gegenbeispiele zu finden. Obgleich der im Artikel gewählte Ansatz vielversprechend zu sein scheint, ist es uns gelungen, Unzulänglichkeiten zu finden und Verkehrsszenarien zu konstruieren, in welchen RSS nicht dafür garantieren kann, dass keine Unfälle stattfinden. Zudem haben wir Ansätze gefunden, wie das Modell ausgebaut und verbessert werden könnte.
Zusammenarbeit mit Corinne Hager Jörin und Florence Yerly 
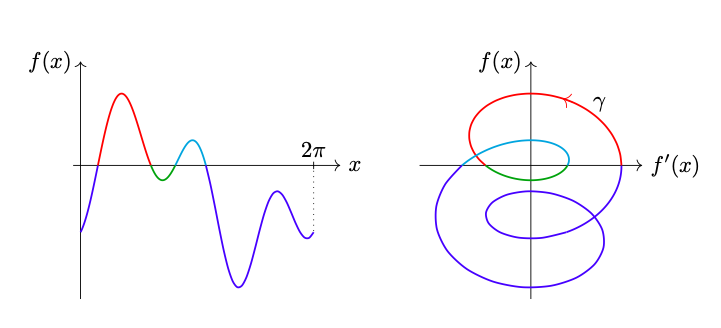
Eine grundlegende Aufgabe in der Mathematik und bei der Bearbeitung mathematischer Modelle, besteht darin, Gleichungen zu lösen. Da Gleichungen oft nicht explizit gelöst werden können, ist es von Interesse, Aussagen über die Lösungsmenge zu machen, beispielsweise über die Kardinalität der Lösungsmenge. In dieser Arbeit wird ein Verfahren angegeben, wie die Anzahl der Lösungen einer reellen Gleichung in einer unbekannten Variablen gezählt werden kann, ohne die Gleichung explizit zu lösen. Dazu wird anhand geometrisch-analytischer Überlegungen ein Integral konstruiert, welches die Anzahl der Lösungen einer Gleichung unter milden Voraussetzungen zählen kann.
N. Hungerbühler, M. Wasem, An integral that counts the zeros of a function, Open Math, 2018
Um die Absatzzahlen verschiedengrosser Verkaufskanäle sinnvoll vergleichen und interpretieren zu können, sind absolute und relative Messungen unzureichend. In diesem Projekt wurde ausgehend von wenigen ökonomisch natürlichen Axiomen eine neue Kennzahl entwickelt, welche die Vergleichbarkeit verschiedener Kanäle auf verschiedenen Skalen ermöglicht. Die Grösse ist auch in Bezug auf die Grundlagenforschung interessant, weil sie einerseits einen Bezug zwischen Grenzfunktionen und ökonomischer Elastizität offenlegt und andererseits als spezielle Cobb-Douglas-Funktion interpretiert werden kann.
Mathematik in Ihren Diensten
mathematical modelling, econometrics, differential geometry
